Все данные в компьютере представлены в двоичном формате, то есть в 0 или 1. Компьютеры или машины понимают биты. Обычно программисту нет дела до операций на битовом уровне. Но иногда нужно погрузиться на более глубокий уровень и работать над битами.

Представление битов

В программировании n-битное целое число сохраняется как двоичное число, которое состоит из n битов. Таким образом, 32-битное целое число состоит из 32 бит, а 64-битное целое число состоит из 64 бит. В языке программирования C ++ тип данных int - 16-битный, 32-битный и 64-битный. Подробней.

Вот битовое представление 32-битного целого числа 10:

00000000000000000000000000001010

В C ++ int либо подписан, либо нет, поэтому битовое представление либо подписано, либо без знака.

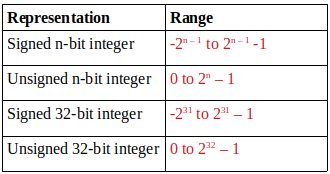
В представлении со знаком первый бит представляет знак числа (0 для положительного и 1 для отрицательного), а оставшиеся n-1 бит содержат величину числа.

Существует связь между подписанным и неподписанным представлением. Подписанный номер -x равно числу без знака 2^n – x,

-x (signed) = 2^n - x (unsigned)

int a = -10;
unsigned int b = a;
std::cout << a << "\n"; /* -10 */
std::cout << b << "\n"; /* 4294967286 */

В подписанном представлении следующий номер после 2^(n – 1) – 1 является -2^n – 1 и в неподписанном представлении следующий номер после 2^n – 1 является 0

Битовые операции

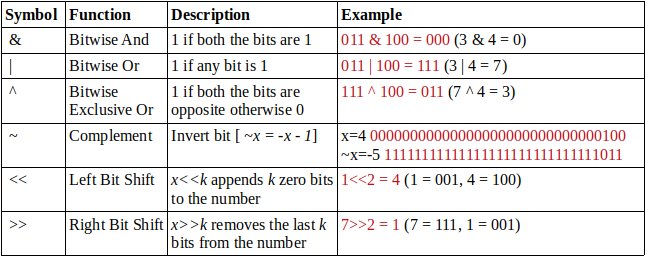
Мы можем использовать & оператор, чтобы проверить, является ли число четным или нечетным. Еслиx & 1 = 0 тогда x даже если x & 1 = 1 Мы также можем сказать, что x делится на 2^k именно тогда, когда x & (2^k – 1) = 0.

x<<k соответствует умножению x по 2^k, а также x>>k соответствует делению x по 2^k округляется до целого числа.

Общие битовые задачи

Двоичное представление неподписанного int :

void binary(unsigned int num)
{
    for(int i = 256; i > 0; i = i/2) {
        if(num & i) 
            std::cout << "1 ";
        else
            std::cout << "0 ";
    }
    std::cout << std::endl;
}

Установка бита в положение:

int set_bit(int num, int position)
{
    int mask = 1 << position;
    return num | mask;
}

Получение бита с позиции:

bool get_bit(int num, int position)
{
    bool bit = num & (1 << position);
    return bit;
}

Сброс бита:

int clear_bit(int num, int position)
{
    int mask = 1 << position;
    return num & ~mask;
}

Представляющие наборы

Биты представления целого числа индексируются 0, и индекс начинается с правой стороны, то есть младшего значащего бита. Таким образом, мы можем представить каждое подмножество множества{0, 1, 2, ..., n-1} как n- битное целое число, и чьи биты указывают, какой элемент принадлежит подмножеству. Если бит в индексе 3 равен 1 и в индексе 4 равен 0 в двоичном представлении числа, то 3 принадлежит подмножеству, а 4 не принадлежит.

Для 32-разрядного целого числа набор равен {0, 1, 2,…, 31}, а подмножество - {1, 3, 4, 8}. Двоичное представление набора:

00000000000000000000000100011010,

а десятичное представление - 2 ^ 8 + 2 ^ 4 + 2 ^ 3 + 2 ^ 1 = 282.

Код для формирования подмножества и добавления к нему элементов:

int add_elements_to_subset()
{
    int subset = 0;
    subset = subset | (1 << 1);
    subset = subset | (1 << 3);
    subset = subset | (1 << 4);
    subset = subset | (1 << 8);
    return subset;
}

Код для печати элементов подмножества:

void printing_subset(int subset)
{
    for (int i = 0; i < 32; i++) 
    {
        if (subset & (1 << i)) std::cout << i << " ";
    }
}

Дополнительные функции

G ++ компилятор обеспечивает следующие функции для подсчета битов:

1. __builtin_clz(x): количество нулей в начале числа
2. __builtin_ctz(x): количество нулей в конце числа
3. _builtin_popcount(x): количество единиц в номере
4. __builtin_parity(x): соотношение (четное или нечетное) числа единиц