Big O Notation используется для описания производительности алгоритма, в частности, используется для описания сценария наихудшего случая. В сценариях существуют другие обозначения, такие как Big Theta (θ) и Big Omega (Ω), используемые для описания сценария среднего случая и сценария наилучшего случая алгоритма.

Но мы, программисты, в основном озабочены наихудшим сценарием, поэтому сосредоточимся на нотации Big O. 

Почему Big O ?

Представьте, что у нас есть несколько человек, работающих над проблемой, у каждого есть свой индивидуальный способ решения проблемы. Но программирование - это не просто решение проблем, а эффективное решение проблем, поэтому, как определить, какие способ решения проблемы является « лучшим »?

Именно здесь Big O помогает вам определить, насколько растет наше время выполнения. Мы делаем это, используя размер ввода, который по стандартам мы называем 'n', и сравниваем его с количеством операций, которые увеличиваются.

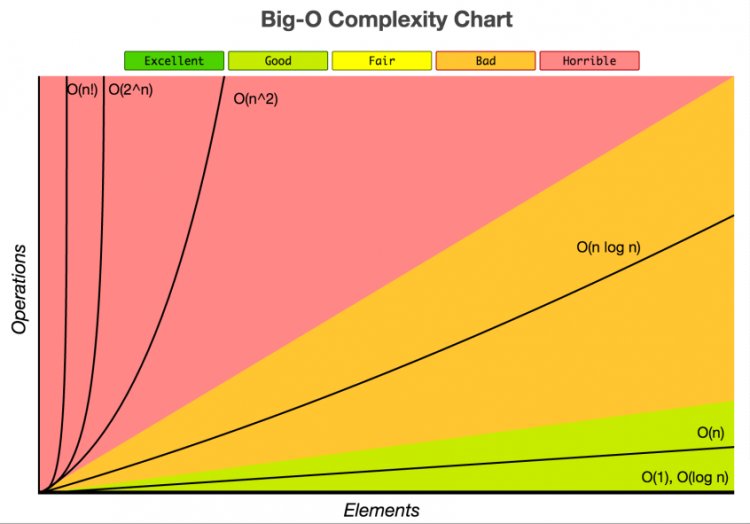
И если вы впервые видите этот сумасшедший синтаксис O (n ^ 2) или O (N log N) и не знаете, что происходит, не беспокойтесь - ниже обьяснение!

PS. На протяжении всей статьи используется JavaScript, но вы можете использовать любой язык по вашему выбору.

O (1)

Первое обозначение Big O, которое у нас есть, это O (1), это означает, что операция всегда будет выполняться за постоянное время независимо от того, насколько велик размер ввода.

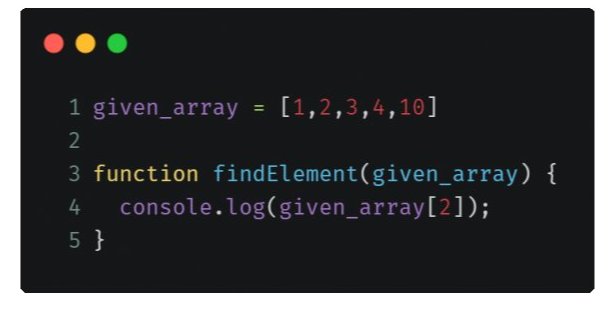
В приведенном выше примере функция просто регистрирует элемент данного массива в консоли. Сколько операций выполняет эта функция, если размер массива увеличен до 1000 или, скажем, до 100 000?

Поскольку мы просто берем один элемент внутри массива, независимо от того, насколько велик размер, время, которое он занимает, всегда остается постоянным или O (1).

O(n)

Здесь мы хотим выяснить, как функция sumOfArray и ее среда выполнения растут по мере увеличения размера ввода. Может быть, массив имеет 1 элемент, может быть, он содержит 100, 1000 или даже миллион элементов в массиве. Как увеличивается эффективность этой функции?

В приведенном выше коде, скажем, у нас есть 10 элементов в массиве, затем для массива из 10 элементов мы сделали проверку 10 раз, чтобы получить желаемое решение. Если бы массив содержал 100 элементов, мы бы перебирали массив 100 раз.

По мере увеличения количества входов количество операций увеличивается линейно. Мы говорим, что приведенный выше код имеет временную сложность O (n) или для решения этой проблемы требуется линейное время. Здесь n просто означает, что Big O зависит от количества входов.

O (N ^ 2)

В случае O (n ^ 2) число выполняемых операций масштабируется пропорционально  квадрату ввода. Это распространено в алгоритмах, которые включают вложенные циклы или итерации.

Допустим, мы хотим найти сумму каждой пары данного массива

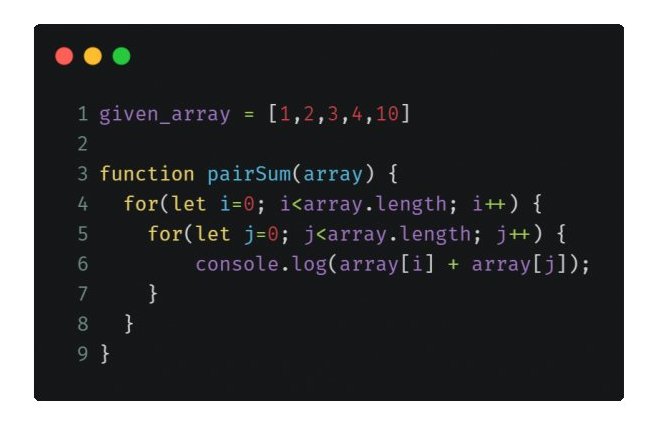
В приведенном выше примере для каждой итерации ' i ' (внешний цикл) мы выполняем n операций внутреннего цикла и работаем с внешним циклом n раз

Или, проще говоря, мы выполняем всего  i * j  операций, или, поскольку мы используем один и тот же ввод,  n * n или n ^ 2

O (2 ^ n)

 O (2 ^ n) обозначает алгоритм, рост которого  удваивается с каждым добавлением к набору входных данных.

Рост этого алгоритма экспоненциальный, скажем, у нас n = 2 входа, затем он будет выполняться 4 раза, при n = 3 он будет выполнять операции 8 раз и так далее.

В приведенном выше примере, если входному параметру n присвоено значение 10, он будет выполнять операции 2 ^ 10 раз, что составляет 1024 раза.

O (log n)

Наиболее распространенный пример демонстрации O (log n) - это классический бинарный поиск.

Теперь бинарный поиск работает с отсортированным набором данных, и он используется для поиска местоположения элемента в данных путем деления ввода пополам с каждой итерацией.

Вместо того, чтобы углубляться в код, давайте рассмотрим простой пример, чтобы понять концепцию. Допустим, у нас есть телефонная книга (да, я знаю, что они устарели), и нам нужно найти контактные данные агента Смита.

Если оставить в стороне матрицу, Смит начинает с S, поэтому где-то во второй половине телефонной книги и почему бы не сказать, что наша телефонная книга составляет 1000 страниц.

Итак, мы открываем середину телефонной книги, видим, что Смит лежит где-то справа от середины, и мы отрываем левую.

Мы  вдвое сократили наш вклад! От 1000 до 500 элементов. Мы снова открываем книгу посередине, выясняем, что Смит лежит где-то с левой стороны от середины, и мы открываем правую сторону, снова вдвое уменьшая ввод с 500 до 250 элементов.

Всего за 2 итерации мы удалили 3 четверти входных данных и у нас осталось n/4 элемента ввода, а за 3 итерации у нас осталось n/8 элементов.

Мы продолжаем в том же духе, пока не найдем наш элемент, поэтому примерно за 10-11 итераций мы прошли набор данных из 1000 элементов и нашли наш элемент, то есть то, что мы называем сложностью логарифмического времени.

Допустим, у нас есть обновленная телефонная книга, и теперь у нас есть 2000 страниц в телефонной книге, общее количество операций увеличилось всего на 1, таким образом, временная сложность бинарного поиска составляет O (log n)

Эта статья охватывает только основы Big O Notation, и, конечно, есть еще много елементов, но это было хорошее начало, и теперь вы знаете основы достаточно, чтобы в них углубиться, если хотите. 

Источник перевода