Если вы программист или уже проходили собеседование, то наверняка знаете о важности знания алгоритмов, чтобы повысить свой уровень программирования или получить шанс получить работу.
При работе с данными сортировка - одна из важнейших задач. Cуществует множество методов сортировки данных, некоторые из них лучше других, некоторые более эффективны для конкретных целей.
В зависимости от метода (рекурсия, итерация, сравнения) или используемых структур данных, можно использовать разные методы сортировки.
Самые популярные методы сортировки Python:
Пузырьковая сортировка:
Пузырьковая сортировка - простой алгоритм сортировки, который работает, меняя местами элементы между собой, если они находятся в неправильном порядке.
Пример :
#Bubble Sort Algorithm
def bubbleSort(data): lenght = len(data)
for iIndex in range(lenght): swapped = False
for jIndex in range(0, lenght - iIndex - 1):
if data[jIndex] > data[jIndex + 1]: data[jIndex], data[jIndex + 1] = data[jIndex + 1], data[jIndex] swapped = True
if swapped == False: break
print(data)
Пузырьковая сортировка используется, когда:
- предпочтителен простой код;
- сложность не имеет значения.
Выборочная сортировка
Выборочная сортировка, или сортировка выбором - это улучшенная версия пузырьковой сортировки, повышающая производительность. Даже в случае, если они имеют одинаковую производительность, выборочная сортировка выполняет меньше замен.
Сортировка выбором работает одним из двух способов: либо ищет наименьший элемент в списке и помещает его в начало списка (обеспечивая правильное расположение элемента), либо ищет самый крупный элемент и помещает его в конец списка.
Пример:
#Selection Sort Algorithm
def selectionSort(data):
for scanIndex in range(0, len(data)):
minIndex = scanIndex
for compIndex in range(scanIndex + 1, len(data)): if data[compIndex] < data[minIndex]: minIndex = compIndex
if minIndex != scanIndex: data[scanIndex], data[minIndex] = data[minIndex], data[scanIndex]
print(data)
Сортировка по выбору используется, когда:
- Сортировка небольших массивов
- Требуется меньше подкачки
Сортировка вставками
Сортировка вставками - это алгоритм сортировки методом "грубой силы", он выполняет меньше сравнений, чем сортировка выбором.
Сортировка вставкой работает, выбирая элемент и сравнивает соседние элементы в массиве, чтобы определить позицию, где первый элемент меньше, а второй больше, чем выбранный элемент. По мере увеличения числа отсортированных элементов алгоритм сравнивает новые элементы с отсортированными и вставляет новый элемент в нужную позицию в списке.
Пример :
#Insertion Sort Algorithm
def insertionSort(data):
for scanIndex in range(1, len(data)): tmp = data[scanIndex]
minIndex = scanIndex
while minIndex > 0 and tmp < data[minIndex - 1]: data[minIndex] = data[minIndex - 1] minIndex -= 1
data[minIndex] = tmp
print(data)
Сортировка вставкой используется, когда:
- Осталось отсортировать несколько элементов;
- Массив небольшой.
Быстрая сортировка
Быстрая сортировка - эффективный алгоритм сортировки. Он использует подход «разделяй-властвуй» для разделения массива на подмассивы, которые рекурсивно вызываются для сортировки элементов.
Для реализации алгоритма быстрой сортировки необходимо выбрать точку поворота, затем разделить массив на два подмассива в соответствии с точкой поворота, а затем расположить их, если они больше / меньше точки поворота. Затем мы сортируем два подмассива и повторяем процесс снова.
Пример :
#Quick Sort Algorithm
def quickSort(data, left, right): if right<= left: return else: pivot = partition(data, left, right) quickSort(data, left, pivot - 1) quickSort(data, pivot + 1, right)
return data
def partition(data, left, right): """This function chooses a pivot point that dertermines the left and right side of the sort""" pivot = data[left] leftIndex = left + 1 rightIndex = right
while True: while leftIndex <= rightIndex and data[leftIndex] <= pivot: leftIndex += 1 while rightIndex >= leftIndex and data[rightIndex] >= pivot: rightIndex -= 1 if rightIndex <= leftIndex: break data[leftIndex], data[rightIndex] = data[rightIndex], data [leftIndex] print(data)
data[left], data[rightIndex] = data[rightIndex], data[left] print(data)
return rightIndex
QuickSort используется, когда:
- Рекурсия необходима и поддерживается;
- Массив небольшой;
- Осталось отсортировать несколько элементов.
Сортировка слиянием
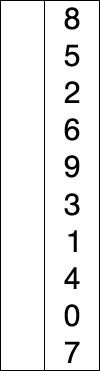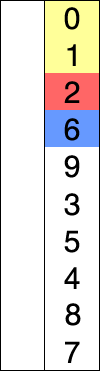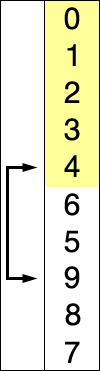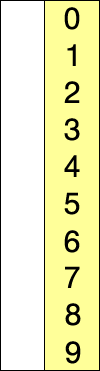
Сортировка слиянием работает, применяя подход «разделяй и властвуй». Сортировка начинается с разбиения набора данных на отдельные части и сортировки частей. Затем он объединяет части таким образом, чтобы гарантировать, что она отсортировала объединенную часть.
Сортировка и объединение продолжаются до тех пор, пока весь набор данных снова не станет единым целым.
Пример:
Пример сортировки слиянием. Сначала разделите список на наименьшую единицу (1 элемент), затем сравните каждый элемент со смежным списком, чтобы отсортировать и объединить два соседних списка. Наконец, все элементы сортируются и объединяются.
#Merge Sort Algorithm
def mergeSort(data): """This function determines whether the list is broken into individual parts"""
if len(data) < 2: return data
middle = len(data)//2
# We break the list in two parts
left = mergeSort(data[:middle]) right = mergeSort(data[middle:])
# Merge the two sorted parts into a larger piece.
print("The left side is: ", left) print("The right side is: ", right)
merged = merge(left, right)
print("Merged ", merged) return merged def merge(left, right): """When left side/right side is empty, It means that this is an individual item and is already sorted."""
#We make sure the right/left side is not empty
#meaning that it's an individual item and it's already sorted.
if not len(left): return left
if not len(right): return right
result = [] leftIndex = 0 rightIndex = 0 totalLen = len(left) + len(right)
#
while (len(result) < totalLen):
#Perform the required comparisons and merge the two parts
if left[leftIndex] < right[rightIndex]: result.append(left[leftIndex]) leftIndex += 1 else: result.append(right[rightIndex]) rightIndex += 1
if leftIndex == len(left) or rightIndex == len(right): result.extend(left[leftIndex:] or right[rightIndex:])
break
return result
Сортировка по сегментам
Алгоритм сортировки по сегментам работает путем разделения массива на сегменты. Затем элементы в каждом сегменте сортируются с использованием любых алгоритмов сортировки или путем рекурсивного вызова алгоритма сортировки сегментами.
Процесс сортировки можно рассматривать как метод разброса-сбора. Элементы сначала раскладываются по сегментам, затем элементы сегментов сортируются. Наконец, элементы собраны по порядку.
Пример:
Код:
#Bucket Sort Algorithm
def bucketSort(data): bucket = []
for iIndex in range(len(data)): bucket.append([])
for jIndex in data: index_bucket = int(10 * jIndex) bucket[index_bucket].append(jIndex) print(bucket)
for iIndex in range(len(data)): #I used the built-in method sorted() to sort the array. bucket[iIndex] = sorted(bucket[iIndex])
kIndex = 0
for iIndex in range(len(data)):
for jIndex in range(len(bucket[iIndex])): data\[kIndex] = bucket[iIndex\][jIndex] kIndex += 1
print(data)
Сортировка сегментами используется в следующих случаях:
- С плавающими числами;
- Входные данные равномерно распределяются по диапазону.
Сортировка Шелла
Сортировка Шелла - это разновидность сортировки вставкой. С помощью этого алгоритма массив сортируется с определенным интервалом на основе выбранной последовательности. Интервал между элементами постепенно уменьшается в зависимости от используемой последовательности. Производительность сортировки оболочки зависит от типа последовательности, используемой для данного входного массива.
Пример:
Gif от GfyCat
Код:
#Shell Sort Algorithm
def shellSort(data, length):
gap = length//2
while gap > 0: for iIndex in range(gap, length):
temp = data[iIndex]
jIndex = iIndex
while jIndex >= gap and data[jIndex - gap] > temp: data[jIndex] = data[jIndex - gap]
jIndex -= gap
data[jIndex] = temp
gap //= 2
print(data)
Сортировка Шелла используется, когда:
- Рекурсия превышает предел.
- Вставка не работает, когда соседние элементы находятся далеко.
Пирамидальная сортировка
Пирамидальная сортировка (ее еще называют сортировкой кучей) - один из лучших методов сортировки без квадратичной сложности наихудшего случая. Это метод сортировки сравнением, основанный на такой структуре данных как двоичная куча. Она похожа на сортировку выбором, где мы сначала ищем максимальный элемент и помещаем его в конец. Далее мы повторяем ту же операцию для оставшихся элементов.
Пирамида - это полное двоичное дерево. Он также проверяет такие правила, как:
- Дети меньше родителей;
- Самый большой / самый маленький элемент находится в корне кучи, в зависимости от того, как вы его отсортировали.
Чтобы создать алгоритм сортировки кучи, мы должны сначала создать кучу массива. Когда закончите, теперь мы можем написать алгоритм сортировки кучи. Преимущество сортировки состоит в том, что значение в корне всегда больше, чем все значения, поэтому мы можем поместить его в конец отсортированного массива, удалить его из кучи, а затем снова скопировать двоичное дерево, чтобы получить большее значение. снова наверху.
Пример:
Код:
#Heap Sort Algorithm
def createHeap(data, length, index):
largest = index left = 2 * index + 1 right = 2 * index + 2
if left < length and data[index] < data[left]: largest = left
if right < length and data[largest] < data[right]: largest = right
if largest != index: data[index], data[largest] = data[largest], data[index] createHeap(data, length, largest)
def heapSort(data): length = len(data)
#We build max heap
for index in range(length, 0, -1): createHeap(data, length, index)
for index in range(length -1, 0, -1): data[index], data[0] = data[0], data[index]
createHeap(data, index, 0)
print(data)
Пирамидальная сортировка отлично подходит, когда вам нужно знать только «самый маленький» (или «самый большой») из коллекции элементов, без накладных расходов на сохранение оставшихся элементов в отсортированном порядке. Например, приоритетная очередь.

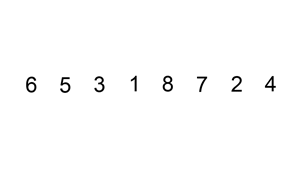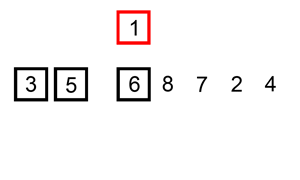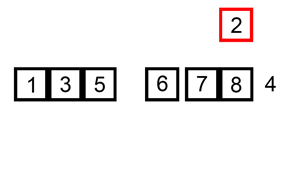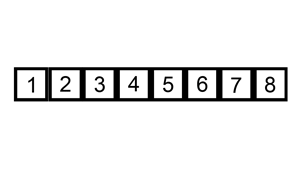
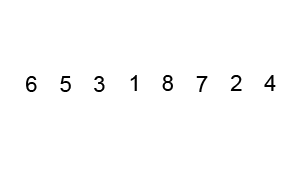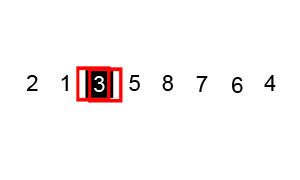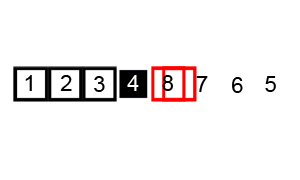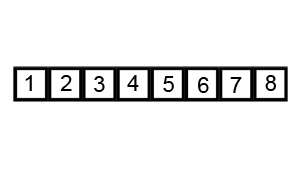






0 комментариев
Добавить комментарий