Многие новички в программировании боятся алгоритмов и даже не начинают их изучать. Но не стоит бояться. Алгоритм - это всего лишь шаги для решения проблемы.
Сегодня рассмотрим основные алгоритмы в простой и наглядной форме.
Не пытайтесь запоминать их, алгоритм больше связан с решением проблем.
Понимание нотации Big O
Нотация Big O - это способ представить временную и пространственную сложность алгоритма.
- Сложность времени: время, затрачиваемое алгоритмом на выполнение.
- Сложность пространства: память, занимаемая алгоритмом.
Есть несколько выражений (обозначений), которые представляют временную сложность алгоритма.
- O (1): постоянная временная сложность. Это идеальный случай.
- O (log n): логарифмическая временная сложность. Если log(n) = xтогда это то же самое, что и10^x
- O (n): линейная временная сложность. Время увеличивается с увеличением количества входов линейно. Например, если один вход занимает 1 мс, то 4 входа потребуют 4 мс для выполнения алгоритма.
- O (n ^ 2): квадратичная временная сложность. Чаще всего это происходит в случае вложенных циклов.
- O (n!): Факторная временная сложность. Это наихудший вариант сенария, которого следует избегать.
Вы должны попытаться написать свой алгоритм так, чтобы он мог быть представлен первыми тремя обозначениями. И последних двух следует избегать.
В следующих разделах этой статьи вы увидите примеры каждой нотации. На данный момент это все, что вам нужно знать.
Алгоритм
Что такое алгоритм и зачем он нужен?
Алгоритм - способ решения проблемы, шаги , процедура или набор правил для решения проблемы.
Пример: алгоритм поисковой системы для поиска данных, относящихся к строке поиска.
Как программист, вы столкнетесь со многими проблемами, которые необходимо решить с помощью этих алгоритмов. Так что лучше, если вы их уже знаете.
Рекурсия
Сама вызывающая функция - это рекурсия. Считайте это альтернативой циклу.
function recursiveFn() {console.log("This is a recursive function");recursiveFn(); } recursiveFn();
В приведенном выше фрагменте кода строка 3 вызывается в строке 3 recursiveFn.
Итак, сколько именно раз будет запускаться эта функция?
Что ж, это создаст бесконечный цикл, потому что его ничто не остановит.
Допустим, нам нужно запустить цикл всего 10 раз. На 11-й итерации функция должна вернуться. Это остановит цикл.
let count = 1; function recursiveFn() {console.log(`Recursive ${count}`);if (count === 10) return;count++;recursiveFn(); } recursiveFn();
В приведенном выше фрагменте строки 4 возвращается и останавливает цикл на счетчике 10.
А теперь посмотрим на более реалистичный пример. Наша задача - вернуть массив нечетных чисел из заданного массива. Это может быть достигнуто несколькими способами, включая цикл for, метод Array.filter и т. д.
Но чтобы продемонстрировать использование рекурсии, используем функцию helperRecursive.
function oddArray(arr) {let result = [];function helperRecursiveFn(arr) {if(arr.length === 0) {return; // 1} else if(arr[0] % 2 !== 0) {result.push(arr[0]); // 2}helperRecursiveFn(arr.slice(1)); // 3}helperRecursiveFn(arr);return result; } oddArray([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]); // OutPut -> [1, 3, 5, 7, 9]
Здесь рекурсивная функция helperRecursiveFn.
- Вернет, если длина массива равна 0.
- Вставит элемент в результирующий массив, если элемент нечетный.
- Вызовет helperRecursiveFn с первым элементом нарезанного массива . Каждый раз первый элемент массива будет разрезан, потому что мы уже проверили его на четность или нечетность.
Например: в первый раз helperRecursiveFn будет вызываться с [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. В следующий раз он будет вызван с помощью [2, 3, 4, 5, 6, 7, 8, 9, 10]и так далее, пока длина массива не станет равной 0.
Алгоритм линейного поиска
Алгоритм линейного поиска довольно прост. Скажем, вам нужно выяснить, существует ли число в данном массиве или нет.
Вы запустите простой цикл for и проверяете каждый элемент, пока не найдете тот, который ищете.
const array = [3, 8, 12, 6, 10, 2]; // Find 10 in the given array. function checkForN(arr, n) {for(let i = 0; i < array.length; i++) {if (n === array[i]) {return `${true} ${n} exists at index ${i}`;}} return `${false} ${n} does not exist in the given array.`; } checkForN(array, 10);
Это алгоритм линейного поиска. Вы ищите каждый элемент в массиве один за другим линейным образом.
Временная сложность алгоритма линейного поиска
Есть только один цикл for, который будет выполняться n раз. Где n (в худшем случае) - длина данного массива. Здесь количество итераций (в худшем случае) прямо пропорционально входу (массив длины).
Следовательно, временная сложность для алгоритма линейного поиска - это линейная временная сложность: O (n) .
Алгоритм двоичного поиска
В линейном поиске вы можете исключать по одному элементу за раз. Но с помощью алгоритма двоичного поиска вы можете удалить сразу несколько элементов. Вот почему бинарный поиск быстрее линейного.
Здесь следует отметить, что двоичный поиск работает только с отсортированным массивом .
Этот алгоритм следует подходу «разделяй и властвуй». Найдем индекс числа 8 в [2, 3, 6, 8, 10, 12].
Шаг 1:
Найдите средний индекс массива.
const array = [2, 3, 6, 8, 10, 12];
let firstIndex = 0;
let lastIndex = array.length - 1;
let middleIndex = Math.floor((firstIndex + lastIndex) / 2); // middleIndex -> 2
Шаг 2.
Убедитесь, что элемент middleIndex> 8. Если это так, это означает, что 8 находится слева от middleIndex. Следовательно, измените lastIndex на (middleIndex - 1).
Шаг 3:
Иначе, если элемент middleIndex <8. Это означает, что 8 находится справа от middleIndex. Следовательно, измените firstIndex на (middleIndex + 1);
if (array[middleIndex] > 8) {lastIndex = middleIndex - 1; } else {firstIndex = middleIndex + 1; }
Шаг 4:
С каждой итерацией middleIndex снова устанавливается в соответствии с новым firstIndex или lastIndex.
Давайте вместе рассмотрим все эти шаги в формате кода.
function binarySearch(array, element) {let firstIndex = 0;let lastIndex = array.length - 1;let middleIndex = Math.floor((firstIndex + lastIndex) / 2); while (array[middleIndex] !== element && firstIndex <= lastIndex) {if(array[middleIndex] > element) {lastIndex = middleIndex - 1;}else {firstIndex = middleIndex + 1} middleIndex = Math.floor((firstIndex + lastIndex) / 2);} return array[middleIndex] === element ? middleIndex : -1; } const array = [2, 3, 6, 8, 10, 12]; binarySearch(array, 8); // OutPut -> 3
Вот визуальное представление приведенного выше кода.
firstIndex = middleIndex + 1;
lastIndex = middleIndex - 1;
array[middleIndex] === 8 // Found It
Временная сложность двоичного поиска
Есть только один цикл while, который будет выполняться n раз. Но здесь количество итераций не зависит от ввода (длины массива).
Следовательно, временная сложность для алгоритма двоичного поиска равна логарифмической временной сложности: O (log n) . И вы можете проверить граф O-нотации. O (log n) быстрее, чем O (n).
Алгоритм Naive Search
Алгоритм Naive Search используется, чтобы определить, содержит ли строка заданную подстроку. Например, проверьте, содержит ли "helloworld" подстроку "owo".
- Первый цикл на основной строке ("helloworld").
- Выполните вложенный цикл для подстроки («owo»).
- Если символ не совпадает, прервать внутренний цикл, иначе продолжить цикл.
- Если внутренний цикл завершен и есть совпадение, то верните true, иначе продолжит работу внешнего цикла.
Вот наглядное представление.
Вот реализация в коде.
function naiveSearch(mainStr, subStr) {if (subStr.length > mainStr.length) return false; for(let i = 0; i < mainStr.length; i++) {for(let j = 0; j < subStr.length; j++) {if(mainStr[i + j] !== subStr[j]) break;if(j === subStr.length - 1) return true;}}return false; }
Теперь давайте попробуем разобраться в приведенном выше коде.
- В строке 2 вернет false, если длина subString больше, чем длина mainString.
- В строке 4 начните цикл на mainString.
- В строке 5 запустите вложенный цикл на subString.
- В строке 6 прервите внутренний цикл, если совпадение не найдено, и перейдите к следующей итерации для внешнего цикла.
- В строке 7 вернуть истину на последней итерации внутреннего цикла.
Временная сложность Naive Search
Внутри цикла есть цикл (вложенный цикл). Оба цикла выполняются n раз. Следовательно, временная сложность для алгоритма наивного поиска равна (n * n) квадратичной временной сложности: O (n ^ 2) .
И, как обсуждалось выше, следует по возможности избегать любой временной сложности выше O (n). В следующем алгоритме мы увидим лучший подход с меньшими временными сложностями.
KMP Алгоритм
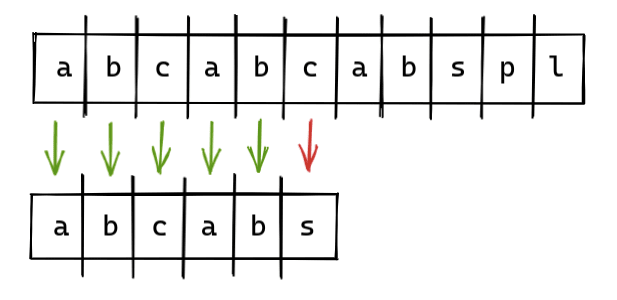
Алгоритм KMP - это алгоритм распознавания образов, и его немного сложно понять. Давайте попробуем определить, содержит ли строка «abcabcabspl» подстроку «abcabs».
Если мы попытаемся решить эту проблему с помощью алгоритма Naive Search , он будет соответствовать первым 5 символам, но не 6-му символу. И нам придется начать заново со следующей итерации, мы потеряем весь прогресс предыдущей итерации.
Итак, чтобы сохранить наш прогресс и использовать его, мы должны использовать что-то, называемое таблицей LPS. Теперь в нашей совпадающей строке «abcab» мы найдем самый длинный префикс и суффикс.
Здесь в нашей строке «abcab» «ab» - это самый длинный префикс и суффикс.
Теперь мы начнем следующую итерацию поиска с индекса 5 (для основной строки). Мы сохранили двух персонажей из нашей предыдущей итерации.
Чтобы определить префикс, суффикс и где начать следующую итерацию, мы используем таблицу LPS.
LPS для нашей подстроки («abcabs») - «0 0 0 1 2 0».
Вот как рассчитать таблицу LPS.
function calculateLpsTable(subStr) {let i = 1; let j = 0;let lps = new Array(subStr.length).fill(0); while(i < subStr.length) {if(subStr[i] === subStr[j]) {lps[i] = j + 1;i += 1;j += 1;} else {if(j !== 0) {j = lps[j - 1];} else {i += 1;}}}return lps; }
Вот реализация в коде с использованием таблицы LPS.
function searchSubString(string, subString) {let strLength = string.length;let subStrLength = subString.length;const lps = calculateLpsTable(subString); let i = 0;let j = 0; while(i < strLength) {if (string[i] === subString[j]) {i += 1;j += 1;} else {if (j !== 0) {j = lps[j - 1];} else {i += 1;}}if (j === subStrLength) return true;} return false; }
Временная сложность алгоритма KMP
Есть только один цикл, который выполняется n раз. Следовательно, временная сложность для алгоритма KMP - это линейная временная сложность: O (n) .
Обратите внимание, как улучшена временная сложность по сравнению с алгоритмом наивного поиска.
Алгоритм пузырьковой сортировки
Сортировка означает переупорядочивание данных в порядке возрастания или убывания. Пузырьковая сортировка - один из многих алгоритмов сортировки.
В алгоритме пузырьковой сортировки мы переставляем большее число в конец, сравнивая каждое число с предыдущим. Вот наглядное представление.
Реализация кода пузырьковой сортировки.
function bubbleSort(array) {let isSwapped; for(let i = array.length; i > 0; i--) {isSwapped = false; for(let j = 0; j < i - 1; j++) {if(array[j] > array[j + 1]) {[array[j], array[j+1]] = [array[j+1], array[j]];isSwapped = true;}} if(!isSwapped) {break;}}return array; }
Попробуем разобраться в приведенном выше коде.
- Цикл от конца массива с переменной i к началу.
- Начните внутренний цикл с переменной j до (i - 1).
- Если array [j]> array [j + 1] поменять местами их.
- Вернет отсортированный массив.
Временная сложность алгоритма пузырьковой сортировки
Существует вложенный цикл, и оба цикла выполняются n раз, поэтому временная сложность для этого алгоритма составляет (n * n), что составляет квадратичную временную сложность O (n ^ 2) .
Алгоритм сортировки слиянием
Алгоритм сортировки слиянием следует подходу «разделяй и властвуй». Это комбинация двух вещей - слияния и сортировки.
В этом алгоритме сначала мы делим основной массив на несколько отдельных отсортированных массивов.
Затем мы объединяем отдельные отсортированные элементы вместе в окончательный массив.
Посмотрим на реализацию в коде.
Объединить отсортированный массив
function mergeSortedArray(array1, array2) {let result = [];let i = 0;let j = 0; while(i < array1.length && j < array2.length) {if(array1[i] < array2[j]) {result.push(array1[i]);i++;} else {result.push(array2[j]);j++;}} while (i < array1.length) {result.push(array1[i]);i++;} while (j < array2.length) {result.push(array2[j]);j++;} return result; }
Приведенный выше код объединяет два отсортированных массива в новый отсортированный массив.
Алгоритм сортировки слиянием
function mergeSortedAlgo(array) {if(array.length <= 1) return array; let midPoint = Math.floor(array.length / 2);let leftArray = mergeSortedAlgo(array.slice(0, midPoint));let rightArray = mergeSortedAlgo(array.slice(midPoint)); return mergeSortedArray(leftArray, rightArray); }
Вышеупомянутый алгоритм использует рекурсию для разделения массива на несколько одноэлементных массивов.
Временная сложность алгоритма сортировки слиянием
Попробуем рассчитать временную сложность алгоритма сортировки слиянием. Итак, взяв наш предыдущий пример ([6, 3, 5, 2]), потребовалось 2 шага, чтобы разделить его на несколько одноэлементных массивов.
**It took 2 steps to divide an array of length 4 - (2^2)
**.
Теперь, если мы удвоим длину массива (8), потребуется 3 шага, чтобы разделить - (2 ^ 3). Значит, удвоение длины массива не привело к удвоению шагов.
Следовательно, временная сложность алгоритма сортировки слиянием равна логарифмической временной сложности O (log n) .
Алгоритм быстрой сортировки
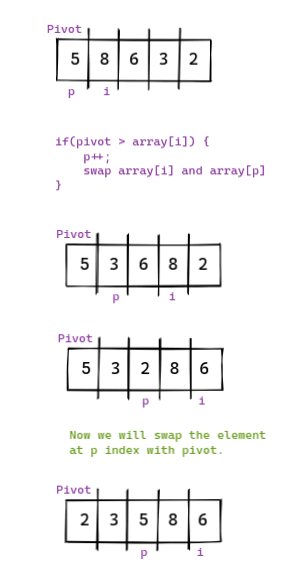
Быстрая сортировка - один из самых быстрых алгоритмов сортировки. При быстрой сортировке мы выбираем один элемент, известный как точка поворота, и перемещаем весь элемент (меньший, чем точка поворота) влево от точки поворота.
Визуальное представление.
Мы будем повторять этот процесс для массива слева и справа от точки поворота, пока массив не будет отсортирован.
Реализация кода
Утилита Pivot
function pivotUtility(array, start=0, end=array.length - 1) {let pivotIndex = start; let pivot = array[start]; for(let i = start + 1; i < array.length; i++) {if(pivot > array[i]) {pivotIndex++;[array[pivotIndex], array[i]] = [array[i], array[pivotIndex]];}} [array[pivotIndex], array[start]] = [array[start], array[pivotIndex]];return pivotIndex; }
Приведенный выше код определяет правильную позицию поворота и возвращает этот индекс позиции.
function quickSort(array, left=0, right=array.length-1) {if (left < right) { let pivotIndex = pivotUtility(array, left, right);quickSort(array, left, pivotIndex - 1);quickSort(array, pivotIndex + 1, right);} return array; }
В приведенном выше коде используется рекурсия, чтобы перемещать точку поворота в правильное положение для левого и правого массива точек поворота.
Временная сложность алгоритма быстрой сортировки
НАИЛУЧШИЙ СЛУЧАЙ: сложность логарифмического времени - O (n log n)
СРЕДНИЙ СЛУЧАЙ: сложность логарифмического времени - O (n log n)
НАИЛУЧШИЙ СЛУЧАЙ: O (n ^ 2)
Алгоритм сортировки Radix
Сортировка Radix также известна как алгоритм сортировки Bucket.
Здесь сначала мы создаем 10 сегментов индекса от 0 до 9. Затем мы берем последний символ в каждом номере и помещаем номер в соответствующий сегмент. Получите новый порядок и повторите для второго последнего символа каждого числа.
Продолжайте повторять описанный выше процесс, пока массив не будет отсортирован.
Реализация в коде.
// Подсчет цифр: в приведенном ниже коде подсчитывается количество цифр в данном элементе.
function countDigits(number) {if(number === 0) return 1; return Math.floor(Math.log10(Math.abs(number))) + 1; }
// Получить цифру: код ниже дает цифру в индексе i справа.
function getDigit(number, index) {const stringNumber = Math.abs(number).toString();const currentIndex = stringNumber.length - 1 - index; return stringNumber[currentIndex] ? parseInt(stringNumber[currentIndex]) : 0; }
// MaxDigit: приведенный ниже фрагмент находит число с максимальным количеством цифр.
function maxDigit(array) {let maxNumber = 0; for(let i = 0; i < array.length; i++) {maxNumber = Math.max(maxNumber, countDigits(array[i]));} return maxNumber; }
// Алгоритм Radix: использует все приведенные выше фрагменты для сортировки массива.
function radixSort(array) {let maxDigitCount = maxDigits(array); for(let i = 0; i < maxDigitCount; i++) {let digitBucket = Array.from({length: 10}, () => []); for(let j = 0; j < array.length; j++) {let lastDigit = getDigit(array[j], i);digitBucket[lastDigit].push(array[j]);} array = [].concat(...digitBucket);} return array; }
Временная сложность алгоритма Radix Sort
Существует вложенный цикл for, и мы знаем, что временная сложность вложенного цикла for равна O (n ^ 2). Но в этом случае оба цикла for не выполняются n раз.
Внешний цикл выполняется k (maxDigitCount) раз, а внутренний цикл - m (длина массива) раз. Следовательно, временная сложность Radix Sort составляет O (kxm) - (где kxm = n) Линейная временная сложность O (n)















0 комментариев
Добавить комментарий