Ця публікація є перекладом статті Тайлера Хоббса - художника, котрий використовує в своїх роботах алгоритми та програмування. Описані в статті ідеї можна використовувати для реалізації власних проектів, пов'язаних зі створенням ексклюзивних графічних візерунків для інтернету і офлайнових продуктів.

***

Векторне поле - потужний і гнучкий інструмент для створення цікавих зображень. Це те, до чого багато програмісти приходять, коли роблять перші алгоритмічні малюнки. Але мало хто знаходить час, щоб дослідити всю різноманітність способів застосування векторних полів. У статті викладені основні відомості про векторні поля, варіанти їх застосування та поради, як отримати збалансоване зображення.

Сітка кутів

Векторне поле будується на сітці, цілком покриває зображення, в кожній точці сітки задається значення кута. У пам'яті комп'ютера сітка представлена двовимірним масивом чисел з плаваючою комою.

Крок. При ініціалізації сітки ви вибираєте крок - відстань між сусідніми елементами. Чим вище розширення, тим менше крок, дрібніше створювані деталі і лінії виходять більш плавними. Але зі зменшенням кроку падає продуктивність. У якості відправної точки кроку підійде порядок 0.5% ширини зображення. Для кроку краще використовувати цілочисельні значення, щоб уникнути помилок округлення чисел з плаваючою комою.

Межі. Останнє, що треба налаштувати - кордони сітки. Виникає спокуса зрівняти їх з межами зображення. Але краще межі сітки віддалити від кордонів кадру. Інакше край зображення буде сильно впливати на «потік» векторного поля. За рахунок віддалення кордонів сітки ми як би фотографуємо потік, що не впливає на його перебіг. Іноді навіть краще почати криві поза зображенням і дозволити їм текти в нього.

Пишемо псевдокод. Давайте припустимо, що у нас є зображення розміром 1000 x 1000 пікселів, і ми хочемо додати 50% -ний запас простору за межами зображення. Ми можемо ініціювати нашу сітку приблизно таким чином:

Ідея опису двовимірної сітки на псевдокоді

left_x = int(width * -0.5)
right_x = int(width * 1.5)
top_y = int(height * -0.5)
bottom_y = int(height * 1.5)

resolution = int(width * 0.01) 

num_columns = (right_x - left_x) / resolution
num_rows = (bottom_y - top_y) / resolution

grid = float[num_columns][num_rows]

default_angle = PI * 0.25

for (column in num_columns) {
    for (row in num_rows) {
        grid[column][row] = default_angle
    }
}

При запуску програми візуалізації в цьому стані, сітка буде виглядати приблизно так:

Сітка за замовчуванням з усіма кутами, встановленими на π / 4. 

Тепер у нас є поле, з яким можна працювати. На жаль, на ньому поки можна малювати тільки прямі лінії. Давайте трохи викривимо його, змінивши опис вищенаведеного циклу:

for (column in num_columns) {
     for (row in num_rows) {
         angle = (row / float(num_rows)) * PI
         grid[column][row] = angle
     }
}

Результат виглядає так:

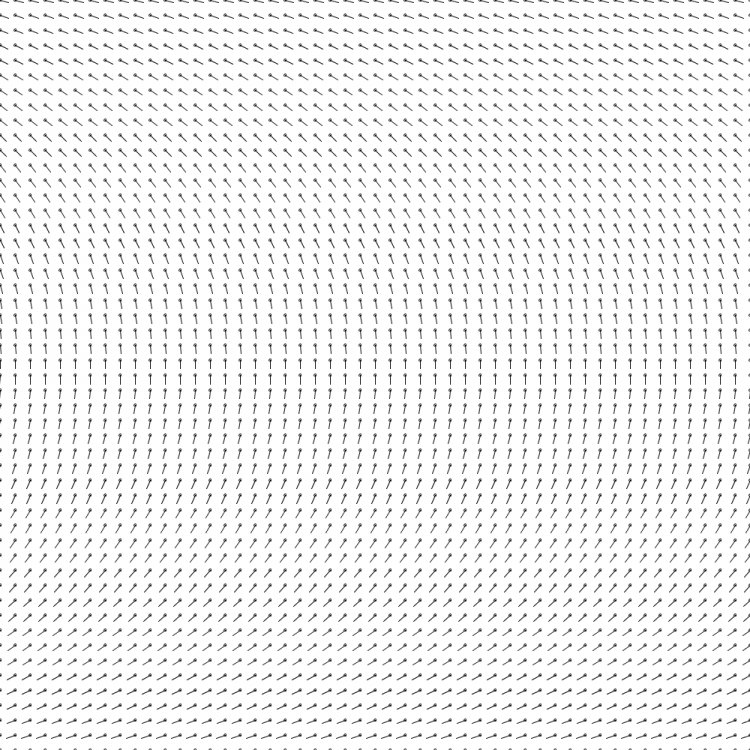
Вигнута сітка

Малюємо лінію у векторному полі

Тепер скористаємося сіткою, щоб намалювати криву:

1. Вибираємо відправну крапку.
2. Знаходимо найближчий вузол сітки, забираємо вказаний у ньому кут.
3. Робимо невеликий крок у відповідному напрямку, малюючи його на зображенні.

Циклічно повторюючи пункти 1-3, малюємо лінію.

// вихідна точка
x = 500
y = 100

begin_curve()

for (n in [0..num_steps]) {

    draw_vertex(x, y)

    x_offset = x - left_x
    y_offset = y - top_y

    column_index = int(x_offset / resolution)
    row_index = int(y_offset / resolution)

    // В цьому місці треба перевірити межі
    grid_angle = grid[column_index][row_index]
   
    x_step = step_length * cos(grid_angle)
    y_step = step_length * sin(grid_angle)

    x = x + x_step
    y = y + y_step
}

end_curve()    

Якщо ми виконаємо наведені дії для однієї кривої, одержимо щось схоже на наступний малюнок:

Одна проста лінія в векторному полі

Нам потрібно вибрати значення для кількох ключових параметрів того, як ми малюємо криві: довжина кроку step_length, число кроків num_steps і координати початкового положення (x, y).

Найпростіше з параметром step_length. Як правило, він повинен бути досить малий, щоб глядач не помічав окремих точок на кривій. Порядка 0,1- 0,5% від ширини зображення. Можна робити більше для швидкого відтворення або менше, якщо на зображенні лінія круто вигинається і повороти повинні залишитися гладкими.

Вибір числа кроків

Значення num_steps кривої впливає на текстуру результату. Короткі лінії більше схожі на хутро, довгі криві - на гладке довге волосся. Нижче пара прикладів запуску однієї і тієї ж програми з різними значеннями num_steps.

Малюнок утворений з коротких ліній

Малюнок утворений з довгих ліній

Зверніть увагу, що перший малюнок відчувається більш грубим, плямистим, шорстким, але плоским, другий - гладкий, спокійний і об'ємний. Око ковзає по другому малюнку, виявляючи закономірності, які поставило векторне поля.

Ще одне міркування стосується змішування кольорів. Більш короткі лінії дозволяють краще розділяти ділянки малюнка з різними кольорами, тоді як лінії достовірніше переносять колір з однієї області в іншу. При грі з багатою палітрою корисно використовувати короткі і середні по довжині лінії, якщо потрібно уникнути розтягнутих областей колірних переходів. Порівняйте:

Приклад з довгими кольоровими лініями

Приклад з короткими кольоровими лініями

З іншого боку, якщо в палітрі використовуються схожі кольори, добре працює перехід до більш довгих кривих. Це дозволяє глядачеві краще відчути їх відмінність:

Вибір стартових позицій

Всі криві повинні десь починатися. Ось три корисних варіанти вибору початкових точок:

1. Регулярна сітка.
2. Рівномірний набір випадкових точок.
3. Упаковка кіл.

Звичайна сітка - найпростіша і жорстка по структурі. Рівномірно розподілені випадкові точки створюють більш пухкий малюнок з згустків і розріджених областей. Підхід з круговою упаковкою має хороший баланс: особливості розподілені рівномірно, але з достатнім числом випадкових варіацій. Якщо ви створюєте чорно-білий малюнок з довгих ліній, ви навряд чи помітите різницю:

регулярна сітка

випадковий розподіл

упаковка кіл

Але при використанні коротких ліній різниця очевидна:

регулярна сітка

випадковий розподіл

упаковка кіл

Спотворення векторного поля

З описаного вище зрозуміло, що викривлення векторного поля задає форму кривих, впливає на петлі, повороти і перекриття ліній. Для спотворення можна використовувати різні підходи. Як приклади розглянемо два антипода: класичний шум Перлина і негладкі спотворення.

Шум Перлина

Шум Перлина дає на двовимірнії площині гладкі безперервні значення. Тому він часто використовується для ініціалізації векторного поля. Цей тип генерації випадкових чисел також має приємну різноманітність «масштабу» шуму, особливості мають різний розмір.

Як це використовувати в коді? Нехай функція noise() повертає значення шуму Перлина (від 0,0 до 1,0) з урахуванням деяких координат. Повернемося до коду ініціалізації. Замість того, щоб вказувати default_angle, можна задавати кути в точках сітки за допомогою noise():

for (column in num_columns) {
  for (row in num_rows) {
      // Для роботи с noise() може знадобитись врахування кроку
      scaled_x = column * 0.005
      scaled_y = row * 0.005

      // використовуємо значение с шумом Перлина в діапазоні від 0.0 до 1.0
      noise_val = noise(scaled_x, scaled_y)

      // транслюємо значення шума в куь між 0 і 2pi
      angle = map(noise_val, 0.0, 1.0, 0.0, PI * 2.0)
      grid[column][row] = angle
  }
}



Результат використання шуму Перлина для сітки кутів

Шум Перлина це хороший інструмент для початку, але краще спробувати придумати щось своє. Хоча б тому, що для подібних проектів така ініціалізація використовується занадто часто.

Негладкі спотворення

Важливий критерій вибору техніки спотворення - чи є вона гладкою чи ні. Тобто чи є перехід між сусідніми векторами плавно, без різких стрибків. Корисно поекспериментувати з негладкими векторними спотвореннями. Простий приклад - почати з шуму Перлина, в якому кут кожного вектора округлено до певного значення, наприклад, кратного π / 10.

Негладкі спотворення при дискретному кроці кута π / 10

Так ми отримуємо більш скульптурні, кам'янисті форми. Якщо обмежитися лише π / 4, вийде щось подібне до грубої гравюри :

Негладкі спотворення при дискретному кроці кута π / 4

Або наприклад, для кожного ряду векторів можна вибрати випадковий кут між 0 і π.

Негладкі спотворення при варіації кроку для різних рядків

Поєднання методів

Кожен може придумати свою гру на векторному полі. Ось ще кілька ідей для натхнення.

Задати дистанцію між кривими. На кожному кроці побудови кривої по сітці можна перевіряти, чи не знаходиться поруч вже існуюча крива. Якщо це так - зупиняємося і починаємо будувати нову криву.

Замість безперервних кривих малювати точки. У наступному прикладі до цього додані перевірки, що дозволяють уникнути «сутичок» кривих.

Злегка спотворювати сітку кутів на певних ітераціях малювання. Це урізноманітнює сімейство одержуваних кривих без їх повного спотворення.

З'єднати сусідні криві і заповнити кольором проміжний простір. Так можна отримати плавні, але не однакові по перетину, структури.

Помістити в кадр об'єкти, які спотворять сітку навколо себе. Всередині «рідкого» векторного потоку з'являються «тверді» об'єкти:

Висновок

Описані підходи, звичайно, не є догмою. Це лише загальні концепції застосування векторних полів для генерації зображень, а також деякий ідеї, які дозволяють отримувати збалансовані малюнки. Більше прикладів використання програмування для створення зображень ви знайдете на сайті автора оригінальної статті.